Computes the power for significance

The power for significance is computed based on the result of the original study, the corresponding variance ratio, and the design prior.

powerSignificance(
  zo,
  c = 1,
  level = 0.025,
  designPrior = c("conditional", "predictive", "EB"),
  alternative = c("one.sided", "two.sided"),
  h = 0,
  shrinkage = 0,
  strict = FALSE
)

Arguments

zo: Numeric vector of z-values from original studies.
c: Numeric vector of variance ratios of the original and replication effect estimates. This is usually the ratio of the sample size of the replication study to the sample size of the original study.
level: Significance level. Default is 0.025.
designPrior: Either "conditional" (default), "predictive", or "EB". If "EB", the power is computed under a predictive distribution, where the contribution of the original study is shrunken towards zero based on the evidence in the original study (with an empirical Bayes shrinkage estimator).
alternative: Either "one.sided" (default) or "two.sided". Specifies if the significance level is one-sided or two-sided. If the significance level is one-sided, then power calculations are based on a one-sided assessment of significance in the direction of the original effect estimates.
h: The relative between-study heterogeneity, i.e., the ratio of the heterogeneity variance to the variance of the original effect estimate. Default is 0 (no heterogeneity). Is only taken into account when designPrior = "predictive" or designPrior = "EB".
shrinkage: Numeric vector with values in [0,1). Defaults to 0. Specifies the shrinkage of the original effect estimate towards zero, e.g., the effect is shrunken by a factor of 25% for shrinkage = 0.25. Is only taken into account if the designPrior is "conditional" or "predictive".
strict: Logical vector indicating whether the probability for significance in the opposite direction of the original effect estimate should also be taken into account. Default is FALSE. Only taken into account when alternative = "two.sided".

Value

The probability that a replication study yields a significant effect estimate in the specified direction.

Details

powerSignificance is the vectorized version of the internal function .powerSignificance_. Vectorize is used to vectorize the function.

References

Goodman, S. N. (1992). A comment on replication, p-values and evidence, Statistics in Medicine, 11, 875--879. doi:10.1002/sim.4780110705

Senn, S. (2002). Letter to the Editor, Statistics in Medicine, 21, 2437--2444.

Held, L. (2020). A new standard for the analysis and design of replication studies (with discussion). Journal of the Royal Statistical Society: Series A (Statistics in Society), 183, 431-448. doi:10.1111/rssa.12493

Pawel, S., Held, L. (2020). Probabilistic forecasting of replication studies. PLOS ONE. 15, e0231416. doi:10.1371/journal.pone.0231416

Held, L., Micheloud, C., Pawel, S. (2022). The assessment of replication success based on relative effect size. The Annals of Applied Statistics. 16:706-720. doi:10.1214/21-AOAS1502

Micheloud, C., Held, L. (2022). Power Calculations for Replication Studies. Statistical Science. 37:369-379. doi:10.1214/21-STS828

Author

Leonhard Held, Samuel Pawel, Charlotte Micheloud, Florian Gerber

Examples

powerSignificance(zo = p2z(0.005), c = 2)
#> [1] 0.9777728
powerSignificance(zo = p2z(0.005), c = 2, designPrior = "predictive")
#> [1] 0.8770464
powerSignificance(zo = p2z(0.005), c = 2, alternative = "two.sided")
#> [1] 0.9580366
powerSignificance(zo = -3, c = 2, designPrior = "predictive",
                  alternative = "one.sided")
#> [1] 0.9062321
powerSignificance(zo = p2z(0.005), c = 1/2)
#> [1] 0.5099361
powerSignificance(zo = p2z(0.005), c = 1/2, designPrior = "predictive")
#> [1] 0.5081131
powerSignificance(zo = p2z(0.005), c = 1/2, alternative = "two.sided")
#> [1] 0.3987708
powerSignificance(zo = p2z(0.005), c = 1/2, designPrior = "predictive",
                  alternative = "two.sided")
#> [1] 0.4170462
powerSignificance(zo = p2z(0.005), c = 1/2, designPrior = "predictive",
                  alternative = "one.sided", h = 0.5, shrinkage = 0.5)
#> [1] 0.2469417
powerSignificance(zo = p2z(0.005), c = 1/2, designPrior = "EB",
                  alternative = "two.sided", h = 0.5)
#> [1] 0.3207855

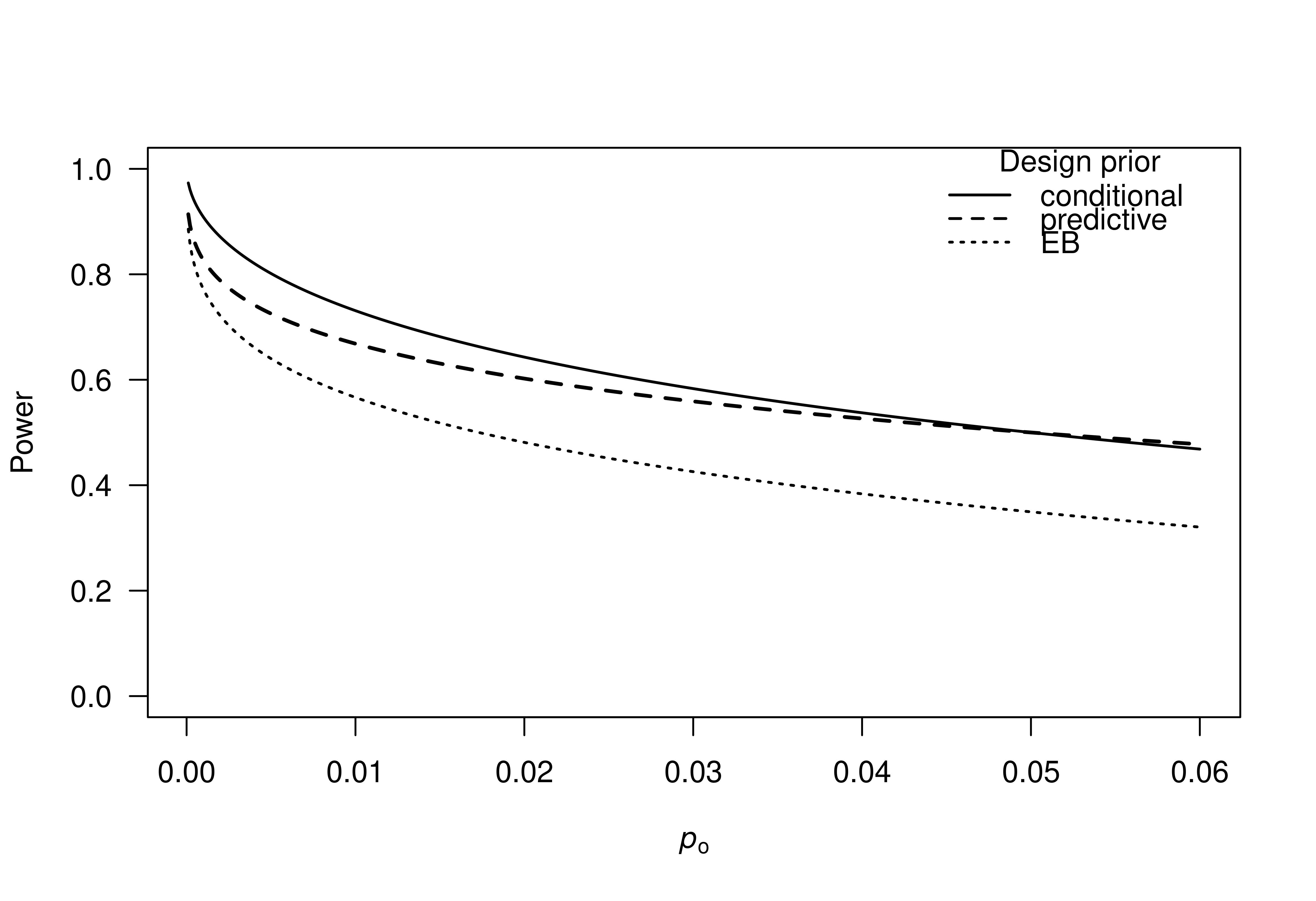
# power as function of original p-value
po <- seq(0.0001, 0.06, 0.0001)
plot(po, powerSignificance(zo = p2z(po), designPrior = "conditional"),
     type = "l", ylim = c(0, 1), lwd = 1.5, las = 1, ylab = "Power",
     xlab = expression(italic(p)[o]))
lines(po, powerSignificance(zo = p2z(po), designPrior = "predictive"),
      lwd = 2, lty = 2)
lines(po, powerSignificance(zo = p2z(po), designPrior = "EB"),
      lwd = 1.5, lty = 3)
legend("topright", legend = c("conditional", "predictive", "EB"),
       title = "Design prior", lty = c(1, 2, 3), lwd = 1.5, bty = "n")