Computes the required relative sample size to achieve replication success with Edgington's method based on power

Source: R/sampleSizeEdgington.R

The relative sample size to achieve replication success with Edgington's method is computed based on the z-value (or one-sided p-value) of the original study, the significance level, the ratio of the weight of the replication study over the weight of the original study, the design prior and the power.

sampleSizeEdgington(
  zo = NULL,
  po = NULL,
  r = 1,
  power,
  level = 0.025,
  designPrior = "conditional",
  shrinkage = 0
)

Arguments

zo

Numeric vector of z-values from original studies.

po

Numeric vector of original one-sided p-values

r

Numeric vector of ratios of replication to original weight.

power

Power to achieve replication success.

level

One-sided significance level. Default is 0.025.

designPrior

Either "conditional" (default) or "predictive".

shrinkage

Numeric vector with values in [0,1). Defaults to 0. Specifies the shrinkage of the original effect estimate towards zero, e.g., the effect is shrunken by a factor of 25% for shrinkage = 0.25. Is only taken into account if the designPrior is "conditional" or "predictive".

Value

The relative sample size to achieve replication success with Edgington's method. If impossible to achieve the desired power for specified inputs NaN is returned.

Details

Either zo or po must be specified.

References

Held, L., Pawel, S., Micheloud, C. (2024). The assessment of replicability using the sum of p-values. Royal Society Open Science. 11(8):11240149. doi:10.1098/rsos.240149

Author

Charlotte Micheloud, Leonhard Held, Samuel Pawel

Examples

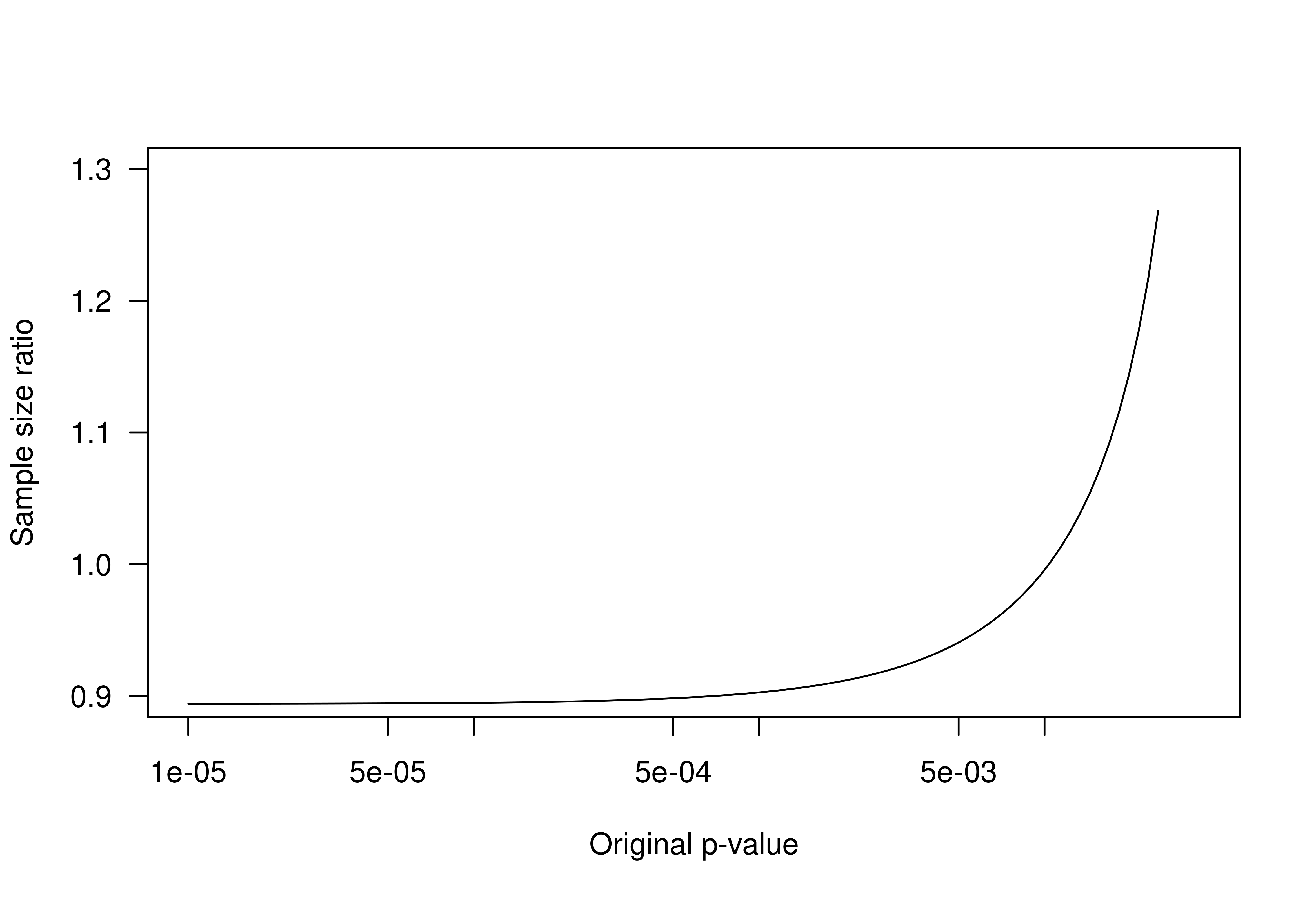
## partially recreate Figure 5 from paper
poseq <- exp(seq(log(0.00001), log(0.025), length.out = 100))
cseq <- sampleSizeEdgington(po = poseq, power = 0.8)
cseqSig <- sampleSizeSignificance(zo = p2z(p = poseq, alternative = "one.sided"),
                                  power = 0.8)
plot(poseq, cseq/cseqSig, log = "x", xlim = c(0.00001, 0.035), ylim = c(0.9, 1.3),
     type = "l", las = 1, xlab = "Original p-value", ylab = "Sample size ratio")